Measuring track curvature
Q: Model railroaders measure curves in inches, which is easily understood. However, prototype railroads measure their curves in degrees. I’m accustomed to degrees as a measure of angles. How do degrees measure radii? – Alan Crouse
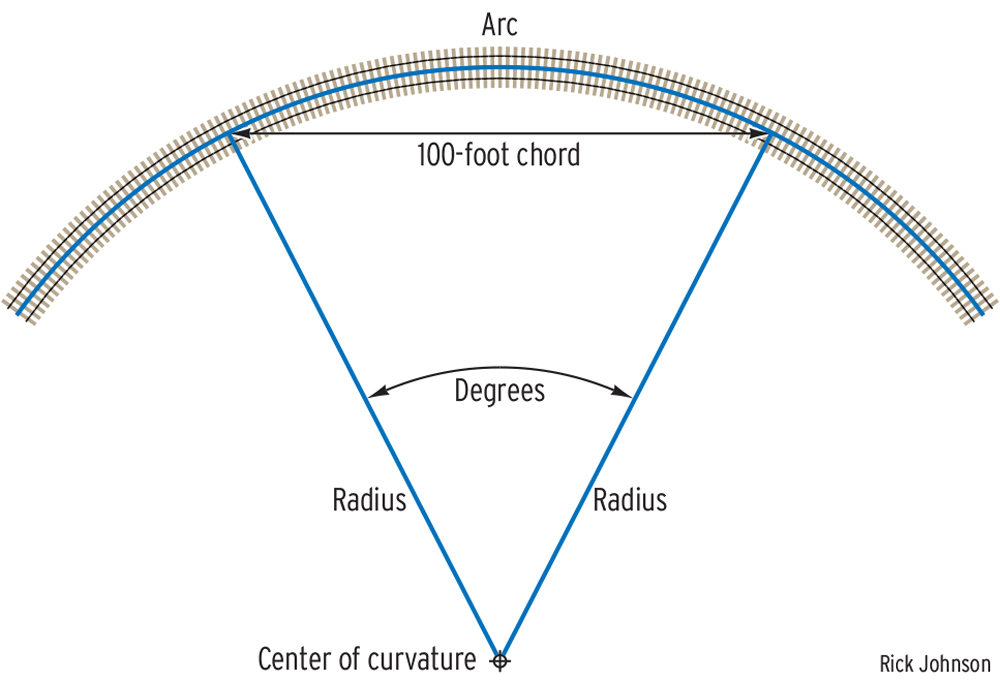
A: We modelers measure track curvature by radius because it’s convenient. It’s usually easy to locate the center of the curve, and the concept of a radius is easy to grasp. However, that’s not as convenient a measurement on the prototype, where the extra-broad curves (by model standards) mean the curve’s center could be hundreds of yards away, on the other side of trees, streets, hills, and buildings from the track. So, prototype railroads measure curvature along a chord.
In geometry, a chord is a straight line connecting the endpoints of a curve. A tangent is a straight line that extends at right angles from the curve’s radius that contacts the curve only at one point; a tangent point is where that straight line meets the curve. The degree of curvature is determined by drawing a 100-foot chord between two tangent points on the curve and measuring how much the track curves between those points. The angle between the two tangent lines is complementary to the angle between the radii, meaning surveyors don’t have to actually find the center point; they can measure the angle between the two tangents and subtract it from 180 degrees. The degree of curvature has an inverse relationship to the curve radius; the higher the degree of curvature, the smaller the radius.
Prototype railroads consider 1 degree of curvature (which works out to a radius of 5,730 feet, or more than a mile – almost 66 feet in HO scale) to be the maximum for a high-speed freight main line. Industrial tracks are generally restricted to less than 12.5 degrees of curvature (for a radius of almost 460 feet, or 5’-3” in HO), though that measurement can vary depending on the railroad’s standards at the time of construction.
If for some reason you’d like to convert your layout’s curve radius to degree measurements, you’re going to need a calculator with trigonometric functions. The formula is 2 arcsin (600/r), where arcsin is the button on your calculator labeled SIN-1 and r is the radius of your curve in scale inches. (If you forget to convert the radius to scale inches and put in some number less than 600, you’ll get an error.) So for example, the curvature of an HO scale 18” radius curve is 2 arcsin (600/1567.8) = 2 arcsin (.3827) = 45 degrees. Which means if you set up 18” radius HO scale sectional track to make a 45-degree curve, the chord across the endpoints of the curve should measure about 100 HO scale feet, or just over 13¾”.
How do we know this works? If you measured all the way across a circle of 18” radius track, that’s an angle of curvature of 180 degrees, and the sine of 180 degrees is 0, which means the diameter and the chord between the end points is the same line. Isn’t math fun? No? Well, then, let’s stick to describing our curves by their radii and never speak of this again.
Send us your questions
Got a question about modeling, operation, or prototype railroading? E-mail it to us at AskTrains@Trains.com. Include your full name and hometown and put “Ask MR” in the subject.
To find more Ask MR articles, click here.